# kirchhoff
## Introduction
This module 'kirchhoff' is part of a series of pyton packages encompassing a set of class and method implementations for a kirchhoff network datatype, which includes a visualization routine based on plotly. The concept is to build kirchhoff networks from networkx graphs, by providing a container for the graphs as well as separate containers for network attributes meant for fast(er) computation in the follow-up modules 'hailhydro' and 'goflow'
## Installation
pip install kirchhoff
## Usage
Generally, just take a weighted networkx graph and read it in as shown. You can plot the network interactivly, with full display of edge and node attributes if desired. Default attributes are 'source'/'potential' for nodes and 'conductivity'/'flow_rate' for edges.
```
import kirchhoff.circuit_init as ki
n=3
G=nx.grid_graph(( n,n,1))
K = ki.initialize_circuit_from_networkx(G)
import kirchhoff.circuit_dual as kid
kid.initialize_dual_flux_circuit_from_minsurf('simple',3)
```
Single and dual networks are supported at the moment, and can be constructed from networkx generator or custom pre-defined types of spatially embedded graphs such as
- crystals/periodic, initialize_circuit_from_crystal(crystal_type='default',periods=1): 'default': simple cubic lattice 3D, 'chain': 1D chain, 'bcc': bcc lattice 3D, 'fcc': fcc lattice 3D,'diamond': diamond lattice 3D,'laves': laves lattice 3D,'trigonal_stack': trigonal lattice stacked and interconnected 3D, 'square': simple cubic lattice 2D, 'hexagonal': hexagonal lattice 2D,'trigonal_planar': trigonal lattice 2D
- random voronoi tesselation, initialize_circuit_from_random(random_type='default',periods=10,sidelength=1): 'default': planar voronoi tesselation with periodic boundaries, 'voronoi_volume': 3D voronoi tesselation with periodic boundaries
- intertwined systems, initialize_dual_circuit_from_minsurf(dual_type='simple',num_periods=2): supporting most of the above in 3D
Further one can define 'flow' and 'flux' circuits for hydrodynamic simulations which are based on Hagen-Poiseuille flow and transport of solutes via advection-diffusion. Doing so will enable more specifically tailored methods for source/solute influx topology control:
```
import kirchhoff.circuit_flow as kfc
kfc.initialize_circuit_from_networkx(G)
kfc.initialize_flow_circuit_from_crystal('simple',3)
kfc.initialize_flow_circuit_from_random(random_type='voronoi_volume')
import kirchhoff.circuit_flux as kfx
kfx.initialize_circuit_from_networkx(G)
kfx.initialize_flux_circuit_from_crystal('simple',3)
kfx.initialize_flux_circuit_from_random(random_type='voronoi_volume')
```
To set node and edge attributes ('source','potential' ,'conductivity','flow_rate') use the set_source_landscape(), set_plexus_landscape() methods of the kirchhoff class and use the class method plot_circuit for plotly output:
```
import kirchhoff.circuit_flow as kfc
K=kfc.initialize_flow_circuit_from_crystal('hexagonal',3)
K.set_source_landscape()
K.set_plexus_landscape()
fig=K.plot_circuit()
fig.show()
```
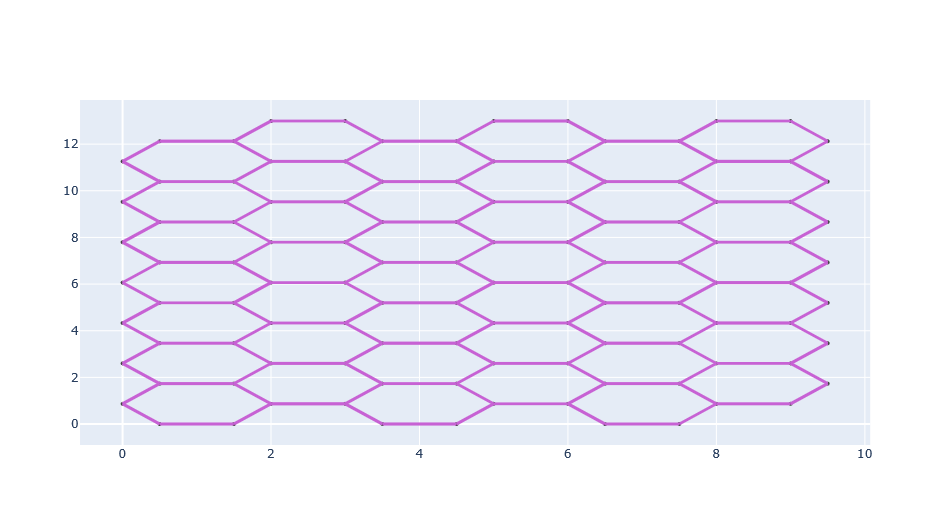
./notebook contains examples to play with in the form of jupyter notebooks
## Requirements
``` pandas ```,``` networkx ```, ``` numpy ```,```plotly```
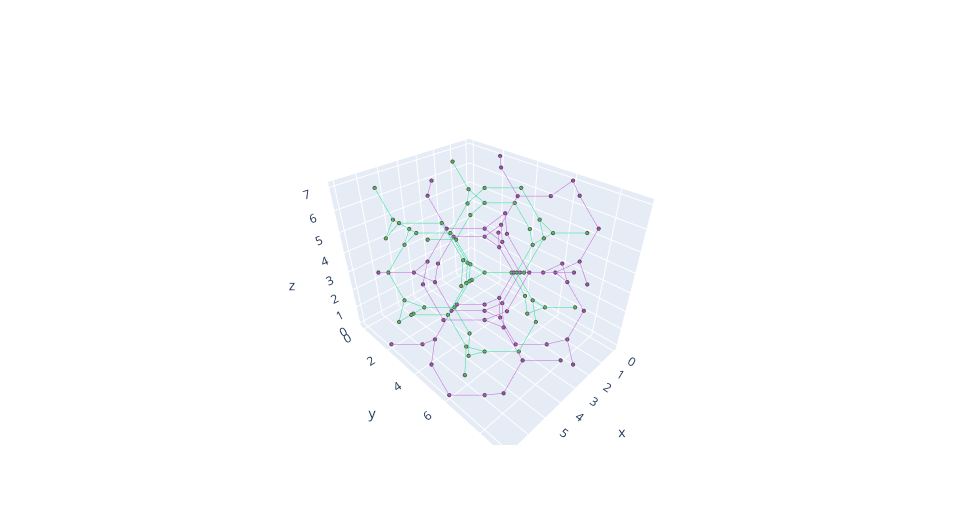
## Gallery


## Acknowledgement
```kirchhoff``` written by Felix Kramer